Policy Evaluation

Consider a sequence of approximate value functions $v_0, v_1, v_2, \dots,$ each mapping $\mathcal{S}^+$ to $\mathbb{R}$. The initial approximation, $v_0$ is chosen arbitrarily, and each successive approximation is obtained by using the Bellman equation for $v_\pi$ as an update rule:

$$\begin{split} v_{k+1}(s)&=\mathbb{E}_\pi[R_{t+1}+\gamma v_k(S_{t+1})|S_t=s]\\ &= \sum_a\pi(a|s)\sum_{s',r}p(s',r|s,a)[r+\gamma v_k(s')], \end{split}$$

for all $s\in\mathcal{S}$.

Policy Improvement

Let $\pi$ and $\pi’$ be any pair of deterministic policies such that, for all $s\in\mathcal{S}$,

$$q_\pi(s,\pi'(s)) \ge v_\pi(s).$$

Then the policy $\pi’$ must be as good as, or better than, $\pi$. That is, it must obtain greater or equal expected return from all states $s\in\mathcal{S}$:

$$v_{\pi'}(s) \ge v_\pi(s).$$

This result is called policy improvement theorem.

Consider the new greedy policy, $\pi’$, given by

$$\begin{split} \pi'(s)&=\underset{a}{\mathrm{argmin}}q_\pi(s,a)\\ &=\underset{a}{\mathrm{argmin}}\mathbb{E}[R_{t+1}+\gamma v_\pi(S_{t+1})|S_t=s, A_t=a]\\ &=\underset{a}{\mathrm{argmin}}\sum_{s',r}p(s',r|s,a)[r+\gamma v_\pi(s')]. \end{split}$$

The greedy policy takes the action that looks best in the short term according to $v_\pi$. By construction, the greedy policy meets the conditions of the policy improvement theorem. The process of making a new policy that improves on an original policy, by making it greedy with respect to the value function of the original policy, is called policy improvement.

In addition, policy improvement must give us a strictly better policy excepy when the original policy is already optimal.

Policy Iteration

Value Iteration

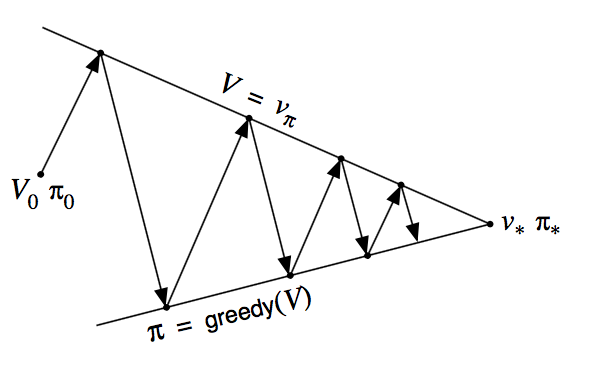
Generalized Policy Iteration

We use the term generalized policy iteration (GPI) to refer to the general idea of letting policy evaluation and policy improvement processes interact, independent of the grandularity and other details of the two processes.